BIC: NOLADE21UEL
Stichwort: PERRYPEDIA
Institut: SK Uelzen Lüchow-Dannenberg
Kontoinhaber: PERRY RHODAN FAN ZENTRALEDeine Spenden helfen, die Perrypedia zu betreiben.Kalup (Einheit)
| Dieser Artikel befasst sich mit der Maßeinheit. Für weitere Bedeutungen, siehe: Kalup. |
Das Kalup ist eine Maßeinheit für eine hyperphysikalische Eigenschaft. Es wird mit dem Einheitenzeichen Kl oder Kp abgekürzt.
- Anmerkung: Der Gebrauch der beiden Abkürzungen ist dabei nicht exakt abgegrenzt. Kp wird anscheinend ausschließlich für hohe und sehr hohe Werte verwendet, während Kl stets bei Kalup-Werten < 1 Anwendung findet und nur selten bei Werten > 1.
Wertemenge
Bei einem Wert von 0 ist der Körper oder Raumbereich frei von jeglichen Hyperraumeinflüssen und kann mittels normaler raumzeitlicher Geometrie beschrieben werden.
Werte zwischen 0 und 1 entstehen, wenn die Hyperfelder um das fragliche Objekt nicht ganz geschlossen sind. Liegt der Wert infinitesimal unter 1 Kalup, so ist das Objekt weder Bestandteil des Normalraums noch des Hyperraums. Man spricht in diesem Fall von einer Semi-Manifestation.
Der Wert von 1 Kalup ist auf den Grenzwert der vollständigen Entmaterialisation eines Körpers definiert.
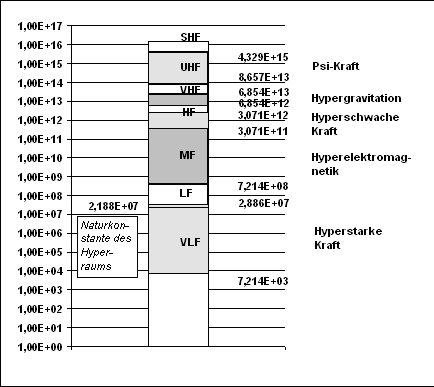
Werte über 1 Kalup kommen nur als ganzzahlige Werte vor und werden benutzt, um verschiedene Hyperphänomene zu klassifizieren. Dabei wird das Kalup analog einer Frequenz benutzt, um die Phänomene mit Frequenzbändern zu unterteilen. Dies ist die so genannte Kalup-Skala oder auch Kalup-Spektrum (siehe Abbildung).
Hef-Skala und Flächendiagramm
Wenn man Hyperphänomene auf andere Art und Weise misst, so kommt man zur Hef-Skala. Lange Zeit dachte man, dass sich diese beiden Skalen nur um einen konstanten Proportionalitätsfaktor von 72,14228 unterscheiden würden.
Bereits in den Jahren nach 430 NGZ formulierte Geoffry Waringer eine Theorie, die auf die Kombination von beiden Skalen in einem ![]() Flächendiagramm hinauslief. Verknüpfungsfaktor ist hier die Strangeness.
Flächendiagramm hinauslief. Verknüpfungsfaktor ist hier die Strangeness.
- → Für weitere Details, siehe: Hyperspektrum.
Weblink
Perry Rhodan Technik Forum: »Das »Kalup« – Eine neue Einheit im Zuge der Halbraumerforschung«
Quelle
... todo ...